Леонардо да Винчи, известният италиански полимат, който нарисува „Мона Лиза“, имал усъвършенствано геометрично разбиране, което изпреварвало времето му. За да нарисува „Витрувианския човек“ през 1490 г. – илюстрация на „идеалното“ човешко тяло – този човек на Ренесанса вероятно се е основавал на математическо съотношение, което е било официално установено едва през 19 век.
Това е една от най-емблематичните картини на всички времена, но в продължение на повече от 500 години никой не можеше да разбере защо да Винчи е избрал точно такива пропорции за ръцете и краката. Един лондонски зъболекар смята, че най-накрая е разгадал загадката.
Още: Хеликоптерът на Леонардо да Винчи може да направи съвременните дронове по-невидими
Разгадана ли е загадката?
Рори Мак Суини е открил важна скрита подробност, скрита в чатала на Витрувианския човек: равностранен триъгълник, който според него може да обясни „едно от най-анализираните, но и най-загадъчни произведения в историята на изкуството“.
„Витрувианският човек“ е частично вдъхновен от писанията на римския архитект Витрувий, който твърди, че идеалното човешко тяло трябва да се побира в кръг и квадрат.
В рисунката на Да Винчи се използва квадрат, за да се изобрази точно „кръстообразна поза“ с изпънати ръце и сгънати крака. Кръгът, от друга страна, обхваща поза, при която ръцете са вдигнати, а краката са разкрачени.
Популярно обяснение е, че да Винчи е избрал пропорциите на Витрувианския човек въз основа на теорията за златното съотношение, но измерванията не съвпадат напълно.
Още: Няма да повярвате какво има на гърба на картината "Мона Лиза" (ВИДЕО)
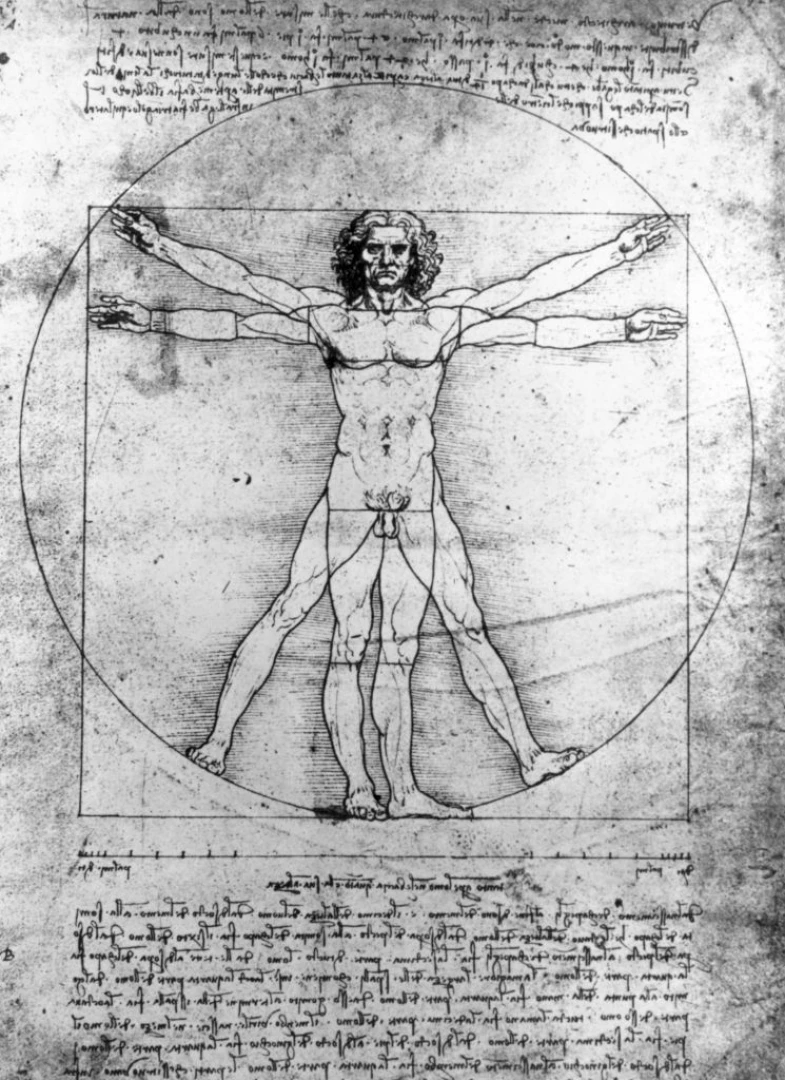
Според Мак Суини „решението на тази геометрична загадка се крие на пръв поглед“.
„Ако разтвориш краката си... и вдигнеш ръцете си толкова, че изпънатите ти пръсти да докоснат линията на върха на главата ти... пространството между краката ще бъде равностранен триъгълник“, пише да Винчи в бележките си за „Витрувианския човек“.
Когато Мак Суини изчислил този триъгълник, той открил, че разстоянието между краката на човека и височината на пъпа му създават съотношение от около 1,64 към 1,65.
Това е много близо до тетраедричното съотношение 1,633 – уникално балансирана геометрична форма, официално установена през 1917 г.
Съотношението се използва за определяне на оптималния начин за подреждане на сфери. Ако четири сфери са свързани възможно най-плътно в пирамидална форма, например, тогава съотношението между височината и основата от техните центрове ще бъде 1,633.
Може би Мак Суини е разпознал значението на това число поради подобен триъгълен принцип, използван в стоматологията. Представен върху човешката челюст, триъгълникът на Бонвил определя оптималното положение за функционирането на челюстта и се използва от 1864 г. Неговото съотношение също е 1,633. Мак Суини не смята, че това е съвпадение.
Подобно на минералите, кристалите и други биологични системи за опаковане, които се срещат в природата, Мак Суини смята, че човешката челюст се организира естествено около тетраедрични геометрии, които максимизират механичната ефективност.
Ако тетраедричното съотношение се повтаря в тялото ни, Мак Суини смята, че това се дължи на факта, че „човешката анатомия е еволюирала според геометрични принципи, които управляват оптималната пространствена организация в цялата вселена“.
Ако Мак Суини е прав, Да Винчи може би е открил универсален принцип, докато е рисувал „Витрувианския човек“.
„Същите геометрични отношения, които се появяват в оптималните кристални структури, биологичните архитектури и координатните системи на Фулер, изглежда са кодирани в човешките пропорции“, пише Мак Суини, „което предполага, че Леонардо е интуитивно разбрал фундаментални истини за математическата природа на самата реалност“.
Остава да се види дали други учени ще се съгласят с Мак Суини, но фактът, че да Винчи споменава равностранното триъгълник в бележките си, подсказва, че това, което се намира между краката на Витрувианския човек, е важно.
Проучването е публикувано в списанието „Journal of Mathematics and the Arts”.